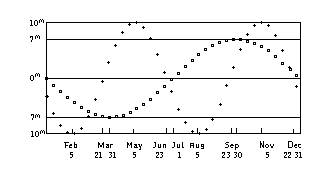
 The variation of the Equation of Time due to Obliquity (crosses)
The variation of the Equation of Time due to Obliquity (crosses)and the variation due to Unequal Motion (squares).
Science and Engineering Research Council
Royal Greenwich Observatory
Information Leaflet No. 13: 'The Equation of Time'
_________________________________________________________
The Equation of Time:
The measurement of time no longer uses sundials but relies on devices, such as clocks, to determine a uniform rate. This rate is calibrated using astronomical observations so that clock time is equivalent to time determined by the mean motion of the Earth.
We know, from modern astronomical observations and from observations of artificial satellites that the Earth's rotation rate is not constant but varies both over the short term and over centuries. These small variations are due to real variations in the rotation of the Earth and are compensated for by inserting leap seconds as appropriate.
If a sundial is used to determine the time, it rapidly becomes apparent that it does not indicate the same time as clock time. The difference amounting to some 16 minutes at certain times of the year. This difference is also seen as an asymmetry in the times of sunrise and sunset. It is called the Equation of Time.
The Equation of Time has two causes. The first is that the plane of the Earth's Equator is inclined to the plane of the Earth's orbit around the Sun. The second is that the orbit of the Earth around the Sun is an ellipse and not a circle.
The Equation of Time due to Obliquity:
The angle between the planes of the Equator and the Earth's orbit around the Sun is called the angle of Obliquity (between 21.55 and 24.18 degrees).
If we assume that the orbit of the Earth is circular, then the apparent motion of the Sun along the great circle, that is the Ecliptic, will be regular, covering equal angles in equal time. We measure apparent Solar time, however, as a projection of this movement onto the [Celestial] Equator.
This projection will be a maximum when the tangents to the great circles of the Equator and the Ecliptic are parallel (at the summer and winter solstices, around June 21 and December 22) and will be a minimum where the tangents to the great circles are at their largest angle (at the equinoxes, around March 21 and September 23).
The Sun will be on the meridian at noon at both solstices and equinoxes and so the Equation of
Time due to Obliquity will be zero at these times.
Between the solstices and the equinoxes the Sun will be slow relative to clock time with minima
near Feb 5 and Aug 5.
Between equinoxes and solstices the Sun will be fast relative to clocks with maxima near May 5 and Nov 5.
The Equation of Time due to Unequal Motion:
The orbit of the Earth around the Sun is an ellipse.
The distance between the Earth and the Sun is a minimum (perigee) on Dec 31 and is greatest (apogee) on July 1.
The Sun's apparent longitude changes fastest when the Earth is closest to the Sun.
The Sun will appear on the meridian at noon on these two dates and so the Equation of Time due
to Unequal Motion will then be zero.
Between Dec 31 and July 1 the Sun will be slow relative to clock time with a minimum around March 31.
Between July 1 and Dec 31 the Sun will be fast relative to clock time with a maximum around Sep 30.
 The variation of the Equation of Time due to Obliquity (crosses)
The variation of the Equation of Time due to Obliquity (crosses)
and the variation due to Unequal Motion (squares).
The Equation of Time:
The total of these two effects gives the Equation of Time,
which is formally defined as the difference between clock time and apparent Solar time.
The Equation of Time takes the form of the curve sketched below.
It is zero on Apr 16, June 15, Sept 1 and Dec 25 and has maxima and minima near Feb 12, May 15, July 27 and Nov 4.
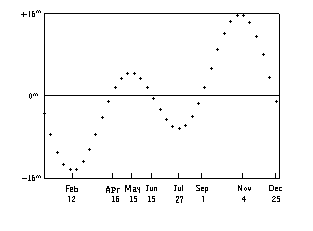 The Equation of Time (the total of the above two effects).
The Equation of Time (the total of the above two effects).
See also; 'Sundials'
Produced by the Information Services Department of the Royal Greenwich Observatory.
PJA Thu Nov 25 13:18:49 GMT 1993
webman@mail.ast.cam.ac.uk
ARVAL's Note:
If we plot the Declination of the Sun versus the Equation of Time for each day of the year, we obtain the Analemma; a figure found in many sundials, maps and geographical globes.
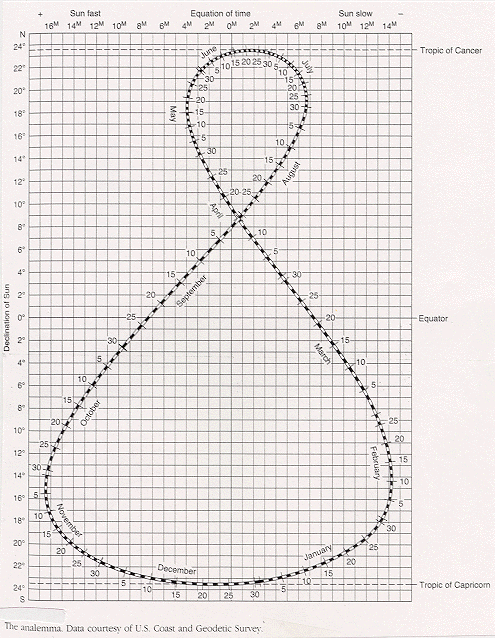
The Analemma shows that for every place between the tropics of Cancer and Capricorn (Lat. 23.45° N and 23.45° S) the Sun will be zenithal twice per year. At the tropic of Cancer, only on June 21st. At the tropic of Capricorn, only on December 22nd. The Sun will never be zenithal outside the tropics.
It also shows that the Sun will be ahead of the clock a maximum of 16 m 33 seg on November 3, and behind a maximum of 14 m 6 seg on February 12.
This Analemma was prepared for Epoch 1950.
For Epoch 2000, the Equation of Time is zero on April 15, June 13, September 1, and December 25,
and has maxima on May 14 and November 3, and minima on February 11 and July 26.
The Equation of Time shifts by 1 day in 24.5 years.
See Equation of time (Wikipedia, the free encyclopedia).
See Analemma (Bob Urschel)
![]() Updated: December 20 '97, June 27 '14
Updated: December 20 '97, June 27 '14
Optimizada para ser vista en fuente Verdana.
Ver Sobre las Páginas en el Web del Observatorio ARVAL.
Back: ARVAL - RGO Leaflets
Messages: